Marco Teorico
Eventos ondularotios:
Movimiento armonico simple:
. El movimiento armonico simple (se abrevia M.A.S) es un movimiento periodico que queda descrito en funcion del timepo for una funcion armonica (seno ó coseno). si la descripcion de un movimiento requiriese mas de una funcion armonica, en general seria un movimiento armonico mas no una M.A.S.
.gif)
se explicaran dos tipos de movimiento armonico simple sistema masa resorte y pendulo simple:
Sistema masa resorte:
consiste en una masa “m” unida a un resorte, que a su vez se halla fijo a una pared, como se muestra en la figura. Se supone movimiento sin rozamiento sobre la superficie horizontal.

El resorte es un elemento muy común en máquinas. Tiene una longitud normal, en ausencia de fuerzas externas. Cuando se le aplican fuerzas se deforma alargándose o acortándose en una magnitud “x” llamada “deformación”. Cada resorte se caracteriza mediante una constante “k” que es igual a la fuerza por unidad de deformación que hay que aplicarle. La fuerza que ejercerá el resorte es igual y opuesta a la fuerza externa aplicada (si el resorte deformado está en reposo) y se llama fuerza recuperadora elástica.
Dicha fuerza recuperadora elástica es igual a :

En el primer dibujo tenemos el cuerpo de masa “m” en la posición de equilibrio, con el resorte teniendo su longitud normal.
Si mediante una fuerza externa lo apartamos de la misma (segundo dibujo), hasta una deformación “x = + A” y luego lo soltamos, el cuerpo empezará a moverse con M.A.S. oscilando en torno a la posición de equilibrio. En este dibujo la fuerza es máxima pero negativa, lo que indica que va hacia la izquierda tratando de hacer regresar al cuerpo a la posición de equilibrio.
Llegará entonces hasta una deformación “x = -A” (tercer dibujo). En este caso la deformación negativa indica que el resorte está comprimido. La fuerza será máxima pero positiva, tratando de volver al cuerpo a su posición de equilibrio.
A través de la Segunda Ley de Newton relacionamos la fuerza actuante (recuperadora) con la aceleración a(t).


Pendulo simple:
Un pendulo simple se define como una particula de masa m suspendida por un hilo de longitud L y de masa despreciable. si la particula se desplaza a una pocision X (angulo que hace el hilo) y luego se suelta el pendulo y comienza a oscilar.
|
|
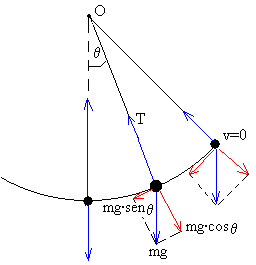
El péndulo describe una trayectoria circular, un arco de una circunferencia de radio l. Estudiaremos su movimiento en la dirección tangencial y en la dirección normal.Las fuerzas que actúan sobre la partícula de masa m son dos
|
Descomponemos el peso en la acción simultánea de dos componentes, mg·senq en la dirección tangencial y mg·cosq en la dirección radial.
-
Ecuación del movimiento en la dirección radial
La aceleración de la partícula es an=v2/l dirigida radialmente hacia el centro de su trayectoria circular.
La segunda ley de Newton se escribe
man=T-mg·cosq
Conocido el valor de la velocidad v en la posición angular q podemos determinar la tensión T del hilo.
La tensión T del hilo es máxima, cuando el péndulo pasa por la posición de equilibrio, T=mg+mv2/l
Es mínima, en los extremos de su trayectoria cuando la velocidad es cero, T=mgcosq0
Datos curiosos "un reloj de pendulo tiene mayor periodo de oscilacion en la luna ya que la gravedad en esta en menor"
Principio de conservación de la energía
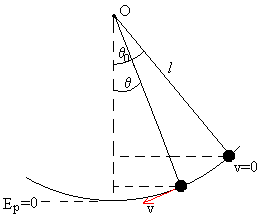
En la posición θ=θ0 el péndulo solamente tiene energía potencial, que se transforma en energía cinética cuando el péndulo pasa por la posición de equilibrio.
Comparemos dos posiciones del péndulo:
En la posición extrema θ=θ0, la energía es solamente potencial.
E=mg(l-l·cosθ0)
En la posición θ, la energía del péndulo es parte cinética y la otra parte potencial
La energía se conserva
v2=2gl(cosθ-cosθ0)
La tensión de la cuerda es
T=mg(3cosθ-2cosθ0)
La tensión de la cuerda no es constante, sino que varía con la posición angular θ. Su valor máximo se alcanza cuando θ=0, el péndulo pasa por la posición de equilibrio (la velocidad es máxima). Su valor mínimo, cuando θ=θ0 (la velocidad es nula).
Ecuación del movimiento en la dirección tangencial
La aceleración de la partícula es at=dv/dt.
La segunda ley de Newton se escribe
mat=-mg·senq
La relación entre la aceleración tangencial at y la aceleración angular a es at=a ·l. La ecuación del movimiento se escribe en forma de ecuación diferencial
(1)
Medida de la aceleración de la gravedad
Cuando el ángulo q es pequeño entonces, senq » q , el péndulo describe oscilaciones armónicas cuya ecuación es
q =q0·sen(w t+j )
de frecuencia angular w2=g/l, o de periodo
La ley de la gravitación de Newton describe la fuerza de atracción entre dos cuerpos de masas M y m respectivamente cuyos centros están separados una distancia r.
La intensidad del campo gravitatorio g, o la aceleración de la gravedad en un punto P situado a una distancia r del centro de un cuerpo celeste de masa M es la fuerza sobre la unidad de masa g=F/m colocada en dicho punto.
su dirección es radial y dirigida hacia el centro del cuerpo celeste.
En la página dedicada al estudio del Sistema Solar, proporcionamos los datos relativos a la masa (o densidad) y radio de los distintos cuerpos celestes.
Ejemplo:
Marte tiene un radio de 3394 km y una masa de 0.11 masas terrestres (5.98·1024 kg). La aceleración g de la gravedad en su superficie es
Tenemos dos procedimientos para medir esta aceleración
Cinemática
Se mide con un cronómetro el tiempo t que tarda en caer una partícula desde una altura h. Se supone que h es mucho más pequeña que el radio r del cuerpo celeste.
Oscilaciones
Se emplea un instrumento mucho más manejable, un péndulo simple de longitud l. Se mide el periodo de varias oscilaciones para minimizar el error de la medida y se calculan el periodo P de una oscilación. Finalmente, se despejag de la fórmula del periodo.
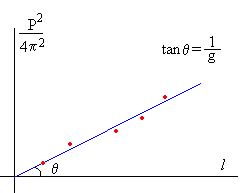
De la fórmula del periodo establecemos la siguiente relación lineal.
Se representan los datos "experimentales" en un sistema de ejes:
P2/(4p2) en el eje vertical y
La longitud del péndulo l en el eje horizontal.
La pendiente de la recta es la inversa de la aceleración de la gravedad g.
Tematicas Segundo periodo:
Sonido

Cualidades del sonido:
La altura o tono. Está determinado por la frecuencia de la onda. Medimos esta característica en ciclos por segundos o Hercios (Hz). Para que podamos percibir los humanos un sonido, éste debe estar comprendido en la franja de 20 y 20.000 Hz. Por debajo tenemos los infrasonidos y por encima los ultrasonidos.
La intensidad. Nos permite distinguir si el sonido es fuerte o débil. Está determinado por la cantidad de energía de la onda. Los sonidos que percibimos deben superar el umbral auditivo (0 dB) y no llegar al umbral de dolor (140 dB). Esta cualidad la medimos con el sonómetro y los resultados se expresan en decibeles (dB).
La duración. Esta cualidad está relacionada con el tiempo de vibración del objeto. Por ejemplo, podemos escuchar sonidos largos, cortos, muy cortos, etc..
El timbre. Es la cualidad que permite distinguir la fuente sonora. Cada material vibra de una forma diferente provocando ondas sonoras complejas que lo identifican. Por ejemplo, no suena lo mismo un clarinete que un piano aunque interpreten la misma melodía.
CUERDAS SONORAS
Una cuerda es el elemento vibratorio que origina el sonido en los instrumentos musicales de cuerda, tales como la guitarra, el arpa, el piano, el contrabajo o miembros de la familia de los violines, descendientes lejanos de las antiguas vihuelas.
Las cuerdas son segmentos formados por un material flexible que permanecen en tensión de modo que puedan vibrar libremente, sin entorpecimiento que provocase una distorsión de la onda acústica.
Las cuerdas pueden ser lisas, que constan de un material único como acero, nailon, oro o tripas de animales; o bien pueden poseer un interior de seda, o nailon y entorchadas con hilos de acero, cobre, plata u oro en el caso de las notas más agudas del violín. Este entorchado tiene la misión de añadir cierto peso y homogeneidad en la vibración de modo que la cuerda alcance la altura sonora deseada, mientras la mantiene lo suficientemente delgada y flexible para tocar.
ONDA SONORA
Una onda sonora es una onda longitudinal perceptible como sonido. Si se propaga en un medio elástico y continuo genera una variación local de presión o densidad, que se transmite en forma de onda esférica periódica o cuasiperiódica.
Propagación
Las variaciones de presión, humedad o temperatura del medio, producen el desplazamiento de las moléculas que lo forman. Cada molécula transmite la vibración a la de su vecina, provocando un movimiento en cadena. Esos movimientos coordinados de millones de moléculas producen las denominadas ondas sonoras, que producen en el oído humano una sensación descrita como sonido.
Modo de propagación
El sonido (las ondas sonoras) son ondas mecánicas elásticas longitudinales u ondas de compresión. Eso significa que:
• Para propagarse precisan de un medio (aire, agua, cuerpo sólido) que transmita la perturbación (viaja más rápido en los sólidos, luego en los líquidos, aún más lento en el aire, y en el vacío no se propaga).
Las cuerdas sonoras son medios elásticos que al ser excitados correctamente producirán un sonido.
las cuerdas presentan las siguientes características según el gráfico.
A= Husos
N= Nodos
L= Longitud de la cuerda
n= Numero de armónico.
Las cuerdas presentan frecuencias distintas dependiendo del numero de armónico al que deseemos calcular la frecuencia.
Formula general:
------------------
Donde:
Fn= Frecuencia n
n= numero de armonico
v= constante del sonido (340 m/s2)

Tubos sonoros:
Tubos sonoros
Se llaman tubos sonoros aquellos que contienen una columna gaseosa (columna de aire) capaz de producir sonido al ser convenientemente excitada. El cuerpo sonoro es la columna gaseosa, y no el tubo que la contiene; en efecto, éste tiene la importante función de definir la forma de aquella pero fuera de esto, influye relativamente poco sobre los fenómenos sonoros. Los tubos sonoros pueden ser cerrados, es decir, que poseen una sola abertura y tubos abiertos, que poseen dos o más.
Vibración de la columna de aire contenida en un tubo
Las columnas de aire contenidas en los tubos sonoros se comportan, desde ciertos puntos de vista, como cuerdas musicales, por lo tanto las columnas de aire vibrantes poseen nodos, o sea puntos donde la vibración es nula, y vientres, equidistantes de los anteriores, donde la vibración alcanza su máxima amplitud.
La vibración de las columnas de aire es longitudinal; los nodos serán por tanto, puntos de condensación y los vientres puntos de dilatación o rarefacción; en los extremos cerrados siempre se producen nodos y en los extremos abiertos generalmente se producen vientres. El punto de excitación no puede ser un nodo, pero no necesita ser un vientre, pudiendo estar en un punto intermedio. No es necesario que las aberturas de un tubo coincidan con los extremos, pudiendo éstos estar cerrados y haber una o más aberturas en otras partes del tubo (la gaita).
Una columna de aire puede vibrar con toda su longitud o dividida en segmentos iguales lo mismo que las cuerdas; en el primer caso se obtiene el sonido llamado fundamental, y en los otros los armónicos: segundo, si la columna vibra dividida en mitades; tercero, si vibra en tercios, etc.
Tomando como punto de partida el que en los extremos de un tubo abierto, sólo pueden haber vientres de vibración, el tubo producirá su fundamental cuando vibre con un nodo único en su centro. Cuando el tubo produce su segundo armónico, producirá dos nodos y tres vientres; cuando produce su tercer amónico, producirá tres nodos y 4 vientres, y así sucesivamente.

En los Tubos Cerrados, la onda se forma con un nodo en el extremo cerrado y un vientre en el extremo abierto.

A igualdad de longitud de tubo, el tubo abierto produce un sonido de frecuencia doble que el cerrado. Los tubos abiertos emiten la serie completa de armónicos correspondientes a su longitud, mientras que los cerrados, emiten sólo los armónicos de orden impar. Como tubo cerrado está la Flauta Travesera y como tubos abiertos todos los demás: Clarinetes*, Oboes, Fagotes, Saxofones, Trompetas, Trompas, etc.
Clasificación de los tubos sonoros
Los tubos sonoros se pueden clasificar de las siguientes formas:
- Según el modo de excitación de la columna de aire
- Según la obtención de la escala
- Según su forma interior
formula para tubos abiertos:
Fn= n*Vsonido/2*longitud del tubo
n= armonico
Formula para tubos cerrados:
Fn = 2n+1*Vsonido/4*longitud del tubo

Estos son los armonicos para un tubo abierto, se comportan igual que una cuerda sonora.

Estos son las armonicos para un tubo cerrado, su primer armonico no tiene ningun nodo, el segundo tiene uno, el tercero dos y asi sucesivamente.
Efecto doppler.
¿ Has notado cómo el tono de las sirenas de las ambulancias, de los bomberos o de la policía, cambia a medida que el auto se nos acerca?. La frecuencia es mayor a medida que el auto se nos acerca, luego, cambia súbitamente a una frecuencia menor a medida que se aleja. Este fenómeno es conocido como el Efecto Doppler. (La frecuencia es el número de vibraciones completas por segundo medidas en una posición fija).
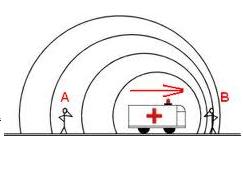
En este dibujo se puede ilustrar este efecto. La fuente sonora se mueve hacia la derecha, con una cierta velocidad, emitiendo ondas que se propagan en círculos centrados en la posición de la fuente (los observadores están ubicados uno adelante y otro atrás de la fuente en el momento que se generan las ondas.)
La frecuencia de la fuente sonora no cambia, pero cuando la fuente se acerca hacia el observador de adelante, más ondas se acumulan entre ellos. La longitud de onda se acorta. Aunque la velocidad del sonido no cambia, la frecuencia del sonido detectado aumenta.
En cambio, cuando la fuente se aleja del detector (de la persona que está detrás), la longitud de onda aumenta y la frecuencia detectada es menor. El efecto Doppler también se presenta si la fuente se encuentra estacionaria, y el detector está en movimiento.
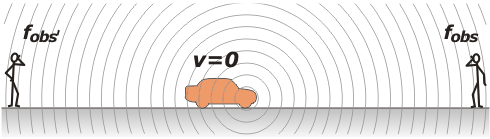
Si la fuente emisora está detenida (sin movimiento) ambos observadores percibirán la misma frecuencia en la misma longitud de onda.
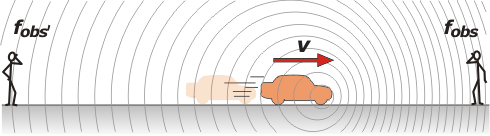
Si la fuente emisora se mueve hacia adelante las ondas se juntan (se acortan) aumentando la frecuencia. Para el observador de atrás, las ondas se alargan (se separan), disminuyendo la frecuencia.
Aplicaciones del Efecto Doppler
El efecto Doppler posee muchas aplicaciones. Los detectores de radar lo utilizan para medir la rapidez de los automóviles y de las pelotas en varios deportes.
Los astrónomos utilizan el efecto Doppler de la luz de galaxias distantes para medir su velocidad y deducir su distancia.
Los médicos usan fuentes de ultrasonido para detectar las palpitaciones del corazón de un feto; los murciélagos lo emplean para detectar y cazar a un insecto en pleno vuelo. Cuando el insecto se mueve más rápidamente que el murciélago, la frecuencia reflejada es menor, pero si el murciélago se está acercando al insecto, la frecuencia reflejada es mayor.
Formula para efecto doppler:
Fo=Ff(V+-Vo/V+-Vf)
Fo= frecuencia del observador
Ff= frecuencoa de la fuente
V= velocidad del sonido 340m/s
Vo= velocidad del observador
Vf= velocidad de la fuente
1.Observador y fuente en reposo
Fo=Ff
2.Observador en reposo fuente se acerca
Fo=Ff(V/V-F)
3.Observador en reposo fuente se aleja
Fo=Ff(V/V+Vf)
4.Fuente en reposo Observador se acerca
Fo=Ff(V+Vo/V)
5.Fuente en reposo observador se aleja
Fo=Ff(V-Vo/V)
6.Ambos se acercan
Fo=Ff(V+Vo/V-Vf)
7.Ambos se alejan
Fo=Ff(V-Vo/V+Vf)
8.El uno persigue al otro
Fo=Ff(V+Vo/V+Vf)

Es un forma de expresar cuando la fuente se acerca y cuando se aleja.
Tematicas tercer periodo
Teoria corpuscular de la luz
el padre de esta teoría es Newton. En contraposición con la teoría ondulatoria del holandés cristian huygens. El uno concebía la luz como materia y el otro como ondas. Al prinicpio prevalecía la teoria de newton, en parte por el gran peso de este físico (seguramente el mejor de la historia) pero las evidencias experimentales acabaron por imponer la teoría ondulatoria. Actualmente se sabe, tras el desarrollo de la física cuántica, que ambos tenían razón, ya que existe una dualidad onda-partícula para todos los entes físicos, y según su tamaño se manifiestan más de una forma que de otra
La luz es un fenómeno ondulatorio de tipo mecánico, como el sonido o las ondas en la superficie del agua.
Son ondas que se propagan en un medio.
En 1801 hace Thomas YOUNG (1773-1829) y En 1822 Augustin J. FRESNEL (1788-1872) experimentos demostrando la interferencia de rayos de luz.
Eso era un apoyo fuerte para la teoría, ya que el modelo corpuscular era incapaz de explicar estos resultados.
En 1864 MAXWELL plantea las ecuaciones del electromagnetismo y se ve que la luz es una onda electromagnética (no una onda mecánica).
Este punto fue confirmado experimentalmente por HERTZ en 1888 al producir y detectar ondas electromagnéticas.
Teoría ondulatoría de Huygens
Huygens propuso que la luz consiste en la propagación de una perturbación ondulatoria del medio. Creía que eran ondas longitudinales similares a las sonoras. Se sabía que la luz puede propagarse en el vacío. Se inventa un medio muy sutil y de perfecta elasticidad que permita dicha propagación. Se le llama éter.
Explicaba fácilmente fenómenos como reflexión y la refracción. Contra esta teoría se argumentaba que si era una onda debía haber fenómenos de difracción e interferencia que no se habían encontrado porque su longitud de onda es muy pequeña y que el resto lo explicaba la teoría corpuscular. La teoría corpuscular gozó de mayor aceptación, fundamentalmente por ser apoyada por Newton, aunque en el siglo XIX acabaría imponiéndose la ondulatoria,

Ley de la reflexión
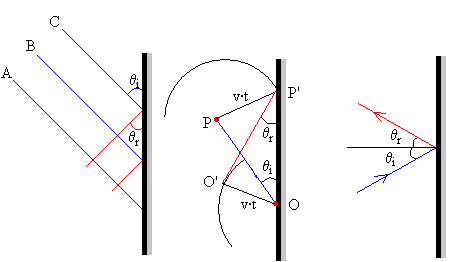
En la parte izquierda de la figura, se muestra el aspecto de un frente de ondas que se refleja sobre una superficie plana. Si el ángulo que forma el frente incidente con la superficie reflectante es θi, vamos a demostrar, aplicando el principio de Huygens, que el frente de ondas reflejado forma un ángulo θr tal que θi= θr.
Las posiciones del frente de ondas al cabo de un cierto tiempo t, se calculan trazando circunferencias de radio v·t con centro en las fuentes secundarias de ondas situadas en varios puntos del frente de onda inicial.
Las ondas secundarias situadas junto al extremos superior A se propagarán sin obstáculo, su envolvente dará lugar a un nuevo frente de ondas paralelo al inicial y situado a una distancia v·t. Las ondas secundarias producidas en el extremo inferior del frente de ondas chocan contra la superficie reflectante, invirtiendo el sentido de su propagación. La envolvente de las ondas secundarias reflejadas da lugar a la parte del frente de ondas reflejado. El frente de ondas completo en el instante t tiene la forma de una línea quebrada.
Tomemos la fuente de ondas secundarias P, de la porción OP del frente de ondas incidente, trazamos la recta perpendicular PP’, tal que PP’=v·t. Con centro en O trazamos una circunferencia de radio v·t. Se traza el segmento P’O’ que es tangente a dicha circunferencia. Este segmento, es la porción del frente de ondas reflejado. De la igualdad de los triángulos OPP’ y OO’P’ se concluye que el ángulo θi es igual al ángulo θr.
Si trazamos las rectas perpendiculares (denominadas rayos) a los frentes de onda incidente y reflejado, se concluye, que el ángulo de incidencia θi formado por el rayo incidente y la normal a la superficie reflectante, es igual al ángulo de reflexión θr formado por el rayo reflejado y dicha normal.
Ley de Snell de la refracción
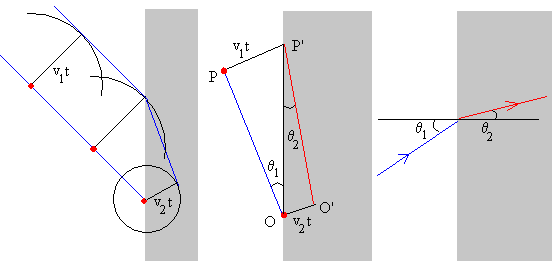
Consideremos un frente de ondas que se acerca a la superficie de separación de dos medios de distintas propiedades. Si en el primer medio la velocidad de propagación de las ondas es v1 y en el segundo medio es v2 vamos a determinar, aplicando el principio de Huygens, la forma del frente de onda un tiempo posterior t.
A la izquierda, se ha dibujado el frente de ondas que se refracta en la superficie de separación de dos medio, cuando el frente de ondas incidente entra en contacto con el segundo medio. Las fuentes de ondas secundarias situadas en el frente de ondas incidente, producen ondas que se propagan en todas las direcciones con velocidad v1 en el primer medio y con velocidad v2 en el segundo medio. La envolvente de las circunferencias trazadas nos da la forma del frente de ondas después de tiempo t, una línea quebrada formada por la parte del frente de ondas que se propaga en el primer medio y el frente de ondas refractado que se propaga en el segundo.
El frente de ondas incidente forma un ángulo θ1 con la superficie de separación, y frente de ondas refractado forma un ángulo θ2 con dicha superficie.
En la parte central de la figura, establecemos la relación entre estos dos ángulos.
-
En el triángulo rectángulo OPP’ tenemos que
v1·t=|OP’|·senθ1
-
En el triángulo rectángulo OO’P’ tenemos que
v2·t=|OP’|·senθ2
La relación entre los ángulos θ1 y θ2 es
![]()
Reflexión total
-
Si v1>v2 el ángulo θ1 > θ2 el rayo refractado se acerca a la normal
-
Si v1<v2 el ángulo θ1 < θ2 el rayo refractado se aleja de la normal
En este segundo caso, para un ángulo límite θc el ángulo de refracción es θ2 =π/2
![]()
El ángulo límite es aquél ángulo incidente para el cual el rayo refractado emerge tangente a la superficie de separación entre los dos medios.
Si el ángulo de incidencia es mayor que el ángulo límite, el seno del ángulo de refracción resulta mayor que la unidad. Esto indica, que las ondas que inciden con un ángulo mayor que el límite no pasan al segundo medio, sino que son reflejados totalmente en la superficie de separación.
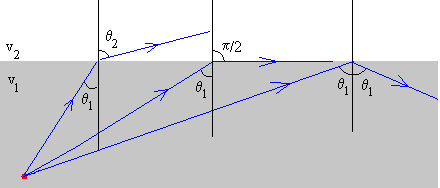
En la figura, observamos que a medida que se incrementa el ángulo de incidencia θ1 el ángulo de refracción aumenta hasta que se hace igual a π/2. Si se vuelve a incrementar el ángulo de incidencia, la onda incidente se refleja en el primer medio.
Índice de refracción
Se denomina índice de refracción, al cociente entre la velocidad de la luz c en el vacío y la velocidad v de la luz en un medio material transparente.
n=c/v
La ley de Snell de la refracción se expresa en términos del índice de refracción
n1·senθ1= n2·senθ2
En la siguiente tabla, se proporcionan datos acerca de los índices de refracción de diversas sustancias
|
Sustancia |
Índice de refracción (línea sodio D) |
|
Azúcar |
1.56 |
|
Diamante |
2.417 |
|
Mica |
1.56-1.60 |
|
Benceno |
1.504 |
|
Glicerina |
1.47 |
|
Agua |
1.333 |
|
Alcohol etílico |
1.362 |
|
Aceite de oliva |
1.46 |
Espejos planos
Una imagen en un espejo se ve como si el objeto estuviera detrás y no frente a éste ni en la superficie. (Ojo, es un error frecuente el pensar que la imagen la vemos en la superficie del espejo).
El sistema óptico del ojo recoge los rayos que salen divergentes del objeto y los hace converger en la retina.
El ojo identifica la posición que ocupa un objeto como el lugar donde convergen las prolongaciones del haz de rayos divergentes que le llegan. Esas prolongaciones no coinciden con la posición real del objeto. En ese punto se forma la imagen virtual del objeto.
La imagen obtenida en un espejo plano no se puede proyectar sobre una pantalla, colocando una pantalla donde parece estar la imagen no recogería nada. Es, por lo tanto virtual, una copia del objeto "que parece estar" detrás del espejo.
El espejo sí puede reflejar la luz de un objeto y recogerse esta sobre una pantalla, pero esto no es lo que queremos decir cuando afirmamos que la imagen virtual no se recoge sobre una pantalla. El sistema óptico del ojo es el que recoge los rayos divergentes del espejo y el cerebro interpreta como procedentes de detrás del espejo (justo donde se cortan sus prolongaciones)
La imagen formada es:
simétrica, porque aparentemente está a la misma distancia del espejo
virtual, porque se ve como si estuviera dentro del espejo, no se puede formar sobre una pantalla pero puede ser vista cuando la enfocamos con los ojos.
del mismo tamaño que el objeto.
derecha, porque conserva la misma orientación que el objeto.
Cuando la luz llega a la superficie de un cuerpo, parte de la luz se refleja y parte entra en el cuerpo donde puede ser absorbida o transmitida, absorbiéndose siempre una parte de ella mientras lo atraviesa (ej. vidrio).
La luz reflejada cumple las leyes de la reflexión.
La cantidad de luz reflejada por un cuerpo depende de:
- La naturaleza de la superficie (composición, estructura, densidad, color, entre otras)
- La textura de la superficie (plana, rugosa, regular, irregular, opaca, pulida , etc.)
- La longitud de onda de la luz, y de si está o no polarizada.
- El ángulo de incidencia de la luz sobre la superficie.
La reflexión de la luz se puede realizar de dos maneras: reflexión irregular o difusa y reflexión regular o especular.

Espejos esfericos
Un espejo esférico está caracterizado por su radio de curvatura R. En el caso de los espejos esféricos solo existe un punto focal F=F´=R/2 cuya posición coincide con el punto medio entre el centro del espejo y el vértice del mismo. Se encontrará a la izquierda del vértice para los espejos cóncavos y a la derecha para los espejos convexos.
El aumento del espejo será A =y´/y y dependerá de la curvatura del espejo y de la posición del objeto.
Formación de imágenes
La construcción de imágenes es muy sencilla si se utilizan los rayos principales:
- Rayo paralelo: Rayo paralelo al eje óptico que parte de la parte superior del objeto. Después de refractarse pasa por el foco imagen.
- Rayo focal: Rayo que parte de la parte superior del objeto y pasa por el foco objeto, con lo cual se refracta de manera que sale paralelo . Después de refractarse pasa por el foco imagen.
- Rayo radial: Rayo que parte de la parte superior del objeto y está dirigido hacia el centro de curvatura del dioptrio. Este rayo no se refracta y continúa en la mismas dirección ya que el ángulo de incidencia es igual a cero.
Hay que distinguir entre los espejos cóncavos y los convexos:
Espejos cóncavos:
-
Objeto situado a la izquierda del centro de curvatura. La imagen es real, invertida y situada entre el centro y el foco. Su tamaño es menor que el objeto.
-
Objeto situado en el centro de curvatura. La imagen es real, invertida y situada en el mismo punto. Su tamaño igual que el objeto.
-
Objeto situado entre el centro de curvatura y el foco. La imagen es real, invertida y situada a la izquierda del centro de curvatura. Su tamaño es mayor que el objeto.
-
Objeto situado en el foco del espejo. Los rayos reflejados son paralelos y la imagen se forma en el infinito.
-
Objeto situado a la derecha del foco. La imagen es virtual, y conserva su orientación. Su tamaño es mayor que el objeto.
 |
a) Objeto situado a la izquierda del centro de curvatura. La imagen es real, invertida y situada entre el centro y el foco. Su tamaño es menor que el objeto. |
| b) Objeto situado en el centro de curvatura. La imagen es real, invertida y situada en el mismo punto. Su tamaño igual que el objeto. | |
| c) Objeto situado entre el centro de curvatura y el foco. La imagen es real, invertida y situada a la izquierda del centro de curvatura. Su tamaño es mayor que el objeto. | |
| d) Objeto situado en el foco del espejo. Los rayos reflejados son paralelos y la imagen se forma en el infinito. | |
| e) Objeto situado a la derecha del foco. La imagen es virtual, y conserva su orientación. Su tamaño es mayor que el objeto. |
Espejos convexos:
Se produce una situación en la que la imagen es virtual, derecha y más pequeña que el objeto.
 |
Se produce una situación en la que la imagen es virtual, derecha y más pequeña que el objeto. |
Lentes Delgadas: convergentes y divergentes
Una lente es un medio transparente limitado por dos superficies curvas. Una onda incidente sufre dos refracciones al pasar a través de la lente.
Hay dos tipos de lentes: convergentes y divergentes.
En la lentes convergentes el foco imagen está a la derecha de la lente, f´ > 0.
En la lentes divergentes el foco imagen está a la izquierda de la lente, f´ < 0.
Las lentes convergentes son más gruesas por el centro que por los extremos, mientras que las divergentes son más gruesas por los extremos que por el centro.
Se define además la potencia de una lente como la inversa de su distancia focal imagen P=1/f´ y mide la mayor o menor convergencia de los rayos emergentes, a mayor potencia mayor convergencia de los rayos. La unidad de potencia de una lente es la dioptría, que se define como la potencia de una lente cuya distancia focal es de un metro.
Lentes convergentes
Tanto en la lentes convergentes como en las divergentes hay dos posibilidades para situar el espejo: más lejos de la lente que el foco objeto (imágenes reales) o entre ambos (imágenes virtuales).
Lentes divergentes
Hay dos posibilidades para situar el espejo: más lejos de la lente que el foco objeto o entre ambos. En ambos casos las imágenes que se forman son virtuales.
La refracción
es el cambio de dirección que experimenta una onda al pasar de un medio material a otro. Solo se produce si la onda incide oblicuamente sobre la superficie de separación de los dos medios y si estos tienen índices de refracción distintos. La refracción se origina en el cambio de velocidad de propagación de la onda.
Un ejemplo de este fenómeno se ve cuando se sumerge un lápiz en un vaso con agua: el lápiz parece quebrado. También se produce refracción cuando la luz atraviesa capas de aire a distinta temperatura, de la que depende el índice de refracción. Los espejismos son producidos por un caso extremo de refracción, denominado reflexión total. Aunque el fenómeno de la refracción se observa frecuentemente en ondas electromagnéticas como la luz, el concepto es aplicable a cualquier tipo de onda.
| Elementos de la cámara Fotográfica |

Objetivo : sistema óptico compuesto por varias lentes, que canaliza la luz que reflejan los objetos situados ante él.
Obturador: sistema mecánico o electrónico que permite el paso de la luz a través del sistema óptico durante un tiempo determinado.
Diafragma: sistema mecánico o electrónico que gradúa la mayor o menor intensidad de luz que debe pasar durante el tiempo que está abierto el obturador.
Sistema de enfoque: gradúa la posición del objetivo, para que la imagen se forme totalmente donde está la placa sensible.
Sistema de deslizamiento de la película: sistema que permite desplazar una nueva película antes de cada toma.
Visor: sistema óptico que permite encuadrar el campo visual que ha de ser fotografiado.
Caja: estuche hermético a la luz y de color contiene todos los elementos anteriores y constituye el cuerpo de la cámara.
| El microscopio simple y compuesto |

Antes de la invención del microscopio,
no era posible la observación de objetos extremadamente pequeños.
El microscopio es un instrumento óptico diseñado para hacer visibles al ojo humano objetos de dimensiones inferiores a 0,1 mm.
Se atribuye su invención al fabricante
de lentes holandés, Zacarías Jansen en el año 1590 y a Galileo en el año 1606, pero Anton Van Leeuwenhoeck fue uno de los primeros que aparte de fabricarlo lo usó con fines biológicos.
 Hoy en día hay varios tipos de microscopios, básicamente se pueden clasificar por el tipo de iluminación que emplean. Pueden ser microscopios que utilizan como fuente de iluminación "radiaciones de luz invisible" y microscopios que utilizan como fuente de iluminación el "espectro de luz visible". |
| El telescopio |
 |
   |
La figura que se ilustra a continuación explica  como se obtiene la imagen como se obtiene la imagen en un telescopio refractor empleando para laobservación astronómica. Las lentes utilizadas son biconvexas tanto en el objetivo como en el ocular y la imagen que se obtiene es virtual e invertida.  |

enfermedad optica miopia
Problema oculares.pptx (100593)
documento de interss para conocer algo sobre tu cuerpo enfermedad correccion



.jpg)